Virtual Arrays for Virtual Worlds

What does it take to simulate a vast, living virtual world in real-time without tanking performance?

In this post, we dig into the lowest and most fundamental levels of our engine architecture, where we represent hundreds of thousands of entities using a blend of data-oriented design, ECS principles, and one of the most underrated tools in the programmer's toolbox: virtual memory.

---

Motivation

The goal of any real-time rendering engine is to create a virtual world of some kind. It could be a game, a simulation, a CAD tool - whatever. At the end of the day you want to represent a virtual world, and that world is made up of elementary building blocks.

Depending on your engine of choice, these building blocks are sometimes called nodes, actors, entities, game objects, or simply objects, but they all refer to the same thing: a collection of data associated to some behavior that represents a thing in your world.

At 3dverse, in our engine, the FTL (for Faster-Than-Light) Engine, we call them entities.

You can find various strategies to represent these entities in code. One of the most prevalent approaches is the ECS (Entity-Component-System) pattern.

The gist of the ECS pattern is to break down your entities into small, reusable components that can be combined in various ways to create complex structures using aggregation instead of inheritance. In a purely ECS architecture, entities are just IDs, components are data-only structures, and systems are stateless functions that operate on the components and alter their state.

Given that entities are the foundation of your virtual world, and that our goal is to create virtual worlds containing potentially millions of entities, we need to be very thoughtful about how we represent them in code.

A lot of articles have been written about ECS, and many of them focus on the theoretical aspects of the pattern, but here we want to focus on the practical side of things: the actual implementation of the ECS pattern in our engine.

Without any further ado, let's dive into the implementation details of our ECS system.

ECS: A Database in Disguise

Another way of looking at the ECS pattern is to see it as a database.

Components are tables, each row in each table represents an instance of that component owned by an entity. A table can also represent entities, this table has a column for every possible component type, a null value means the entity doesn't have that component, otherwise the value is the index of the component in its corresponding table.

Take these Transform and MeshRef components for example:

struct Transform {
    vec3 position;
    quat orientation;
    vec3 scale;
};

struct MeshRef {
    uint32_t meshId;
    uint32_t materialId;
};

The components tables would look like this:

Transform table:

Index	position	orientation	scale
0	(0, 0, 0)	(0, 0, 0, 1)	(1, 1, 1)
1	(1, 0, 0)	(0, 0, 0, 1)	(1, 1, 1)
N	...	...	...

MeshRef table:

Index	meshId	materialId
0	42	2
1	42	6
N	...	...

And the Entity table would look like this:

Entity table:

Index	transformId	meshRefId	...
0	4	null	...
1	0	6	...
N	...	...	...

Naive implementation

This is exactly the way we approached the problem.

Here's the naive code we started with:

struct Entity {
    uint32_t transformId;
    uint32_t meshRefId;
};

struct EntityDatabase {
    std::vector<Transform> transform_table;
    std::vector<MeshRef>   meshRef_table;
    std::vector<Entity>    entity_table;
};

This is actually all you need to get going. By adding a proper API to this basic implementation, you can create entities, add components to them, and iterate over them. It's simple, easy to understand and follows data-oriented design principles.

This is a great way to get started with ECS, and it works well for small worlds with a few hundred or thousand entities that are relatively static.

Issues

As your world grows, this approach quickly reveals its limitations.

The main problem boils down to the way we store our components: std::vector. std::vector is a great data structure for small arrays or large arrays that are rarely changing size. But as soon as you start randomly adding and removing elements from it, it becomes problematic.

This has to do with the way std::vector works internally.

At its core, std::vector is a simple resizable dynamic array with a very straightforward, but very "one-size-fits-all" allocation strategy:

• A new vector starts empty unless you provide an initial size.
• It keeps track of the current size and the capacity of its internal buffer.
• When you add an element to the vector, it starts by checking if the current size is less than the capacity.
  • If it is, it simply adds the element to the end of the vector -> this is our happy, fast path.
  • If it isn't, it allocates a new buffer with a new capacity (growth factor is implementation specific, but it's generally 1.5x or 2x the current capacity), copies/moves all the elements from the old buffer to the new one, deletes the old buffer, and then adds the new element to the end of the vector -> this is the slow path we want to avoid.
• When you remove an element from the vector, there are two strategies:
  • Use std::remove then pop: swaps the element to remove with the last element, and then pops the last element.
  • Use erase: this will shift all the elements after the removed element to the left by one position.

Two issues arise from this:

1. The slow path is very expensive, as it involves allocating a new buffer and copying all the elements from the old buffer to the new one. This is especially problematic when you have a lot of components, as it can lead to fragmentation and performance issues like stuttering.

2. The second issue is that it also invalidates all the pointers to the elements as the buffer has been replaced with a new one. The same problem happens when you remove an element from the vector, it invalidates at least some pointers. This can become a huge headache when introducing parallelism.

So, how do we solve this?

Solution

There is actually a simpler solution than a dynamic array: a fixed size array.

A fixed size array doesn't involve random allocations, and it doesn't require moving things around when adding or removing elements.

Pointers to the elements are always valid, and the memory is contiguous.

The only downside is that you have to know the size of the array in advance, which is not always possible. One solution is to allocate for the worst case scenario, but that would be wasteful.

So how do we get these benefits without the drawbacks?

Enter virtual memory.

Virtual memory is a powerful tool provided by the OS that allows you to acquire a large chunk of memory without actually allocating it.

It does that by letting you reserve a virtual address range and backing it up with physical memory (actual RAM) only when needed. This is perfect for our use case, as it makes the "allocate for the worst case" scenario drawback irrelevant.

A few things to keep in mind when using virtual memory:

• Virtual memory is divided into pages, which are the smallest unit of memory that can be reserved or committed, meaning:
  • You can't reserve less than a page (4 KiB on most systems).
  • You can't commit (allocate physical memory) less than a page (4 KiB on most systems).
• Virtual space is not infinite, so you still need to be careful about how much memory you reserve. On 64-bit Windows it goes up to 128 TB for example.

As the granularity of the allocation is a page, it's not recommended to use this for small arrays. But in our case, we are dealing with thousands of components so it's a perfect fit.

Virtual address space is divided into physical pages.

So by combining virtual memory with fixed size arrays we get the virtual array.

Without further ado, let's dive into the implementation details:

Building the Virtual Array

Virtual Memory

First, let's take a look at how to use virtual memory in C++.

Virtual memory is a low level API provided by the OS, so it's not part of the C++ standard library.

On Windows you can use the VirtualAlloc API to reserve and commit memory. The API is pretty simple to use:

Reserve address space (no physical memory yet):

void *reserve(int64_t sizeInByte) {
    return VirtualAlloc(nullptr, sizeInByte, MEM_RESERVE, PAGE_READWRITE);
}

Commit memory (backed by physical RAM):

void *commit(void *pAddr, int64_t size) {
    return VirtualAlloc(pAddr, size, MEM_COMMIT, PAGE_READWRITE);
}

Reset memory (releases physical RAM but keeps the address):

void *reset(void *pAddr, int64_t size) {
    return VirtualAlloc(pAddr, size, MEM_RESET, PAGE_NOACCESS);
}

Release memory and address space completely:

bool deallocate(void *pAddr) {
    return VirtualFree(pAddr, 0, MEM_RELEASE) == TRUE;
}

On posix systems you can use mmap to achieve the same result.

One of the benefits of VirtualAlloc is that the memory is automatically zeroed out when you commit it.

Template class

Let's start by creating a simple template class that will represent our virtual array.

We'll also define a few compile-time constants to help us with the implementation:

template<typename T, size_t N>
class virtual_array {
public:
    static constexpr size_t PAGE_SIZE = 0x1000; // 4 KiB
    static constexpr size_t ELEMENT_SIZE = sizeof(T);
    static_assert(ELEMENT_SIZE <= PAGE_SIZE,
        "Element cannot span multiple pages.");

    static constexpr size_t ELEMENTS_PER_PAGE = PAGE_SIZE / ELEMENT_SIZE;
    static constexpr size_t MAX_PAGE_COUNT = (N / ELEMENTS_PER_PAGE)
                                    + ((N % ELEMENTS_PER_PAGE) == 0 ? 0 : 1);
private:
    T *pStart_;
    T *pCurrent_;
    T *pLast_;
};

The constants should be self explanatory, but let's go through them quickly:

• PAGE_SIZE: the size of a page in bytes (4 KiB).
• ELEMENT_SIZE: the size of one element of type T in bytes.
• ELEMENTS_PER_PAGE: the number of elements that can fit in a single page.
• MAX_PAGE_COUNT: the maximum number of pages we need to hold the N elements. Note that it's rounded up to the next multiple of PAGE_SIZE if N is not a multiple of PAGE_SIZE.

We also need to define a few pointers for bookkeeping:

• pStart_: points to the start of the virtual space. It shouldn't be modified after the initial allocation.
• pCurrent_: points to the first free element in the array.
• pLast_: points to the end of the last committed page.

Let's check the constructor:

virtual_array() {
    const auto sizeInByte = N * sizeof(T);
    pStart_ = VirtualAlloc(nullptr, sizeInByte, MEM_RESERVE,
        PAGE_READWRITE);
    pCurrent_ = pLast_ = pStart_;
}

This reserves enough address space for N elements of type T, but doesn't commit any physical memory yet, hence the MEM_RESERVE flag.

Note that VirtualAlloc will automatically round up the size to a multiple of the page size. Example: if you reserve 3 KiB of memory, it will actually reserve 4 KiB.

Let's also add a destructor to release the memory when we're done with it:

~virtual_array() {
    if constexpr (!std::is_trivially_destructible_v<T>()) {
        while (pCurrent_ != pStart_) {
            (*pCurrent_).~T();
            --pCurrent_;
        }
    }
    VirtualFree(pStart_, 0, MEM_RELEASE);
    pStart_ = nullptr;
}

The destructor will call the destructor of each element in the array, and then release the memory using VirtualFree. Note that we only call the destructor if the type is not trivially destructible.

Insertion

Now that we have reserved the address space, we need to implement the insertion that will actually trigger the allocation of physical memory when needed.

Let's start by adding a function to grow the array by one page:

void grow() {
    // Commit a new page worth of elements
    VirtualAlloc(pLast_, PAGE_SIZE, MEM_COMMIT, PAGE_READWRITE);
    pLast_ += ELEMENTS_PER_PAGE;
}

We will use pLast_ to loosely track the end of the last committed page. I say loosely, because pLast_ actually points to the end of the last element of the last committed page, not the end of the last committed page itself.

Luckily for us, VirtualAlloc will do the right thing and commit the next page regardless of whether pLast_ aligns perfectly with a page boundary or not, committing PAGE_SIZE bytes will always commit the next page.

Now that we have a way to grow the array, let's implement the insertion function:

template<typename... _Args>
T* emplace(_Args &&...args) {
    if (pCurrent_ == pLast_) {
        grow();
    }
    assert(pCurrent_ < pLast_);

    new (pCurrent_) T(std::forward<_Args>(args)...);
    return pCurrent_++;
}

We follow the same pattern as the standard library: a variadic template function that takes the arguments to construct the element in place.

Before doing that, we check if the current pointer has reached the last element of the last committed page. If it has, we just call grow() to commit a new page worth of elements.

Usage

This simple implementation is based on a few assumptions:

The array grows by committing a new page worth of elements when the last committed page is full. For this to be efficient we rely on the fact that our components are relatively small and that we can fit a lot of them in a single page.

With this, our initial implementation of the ECS becomes simply:

struct Transform {
    vec3 position;     // 12 bytes
    quat orientation;  // 16 bytes
    vec3 scale;        // 12 bytes
}; // Total: 40 bytes

virtual_array<Transform, 10'000'000> transforms;

// At this point: no physical memory is committed.
// We just reserved enough address space for 10 million elements.

transforms.emplace(Transform{...});
// The first insertion commits one 4 KiB page (enough for 102 elements of 40
// bytes).

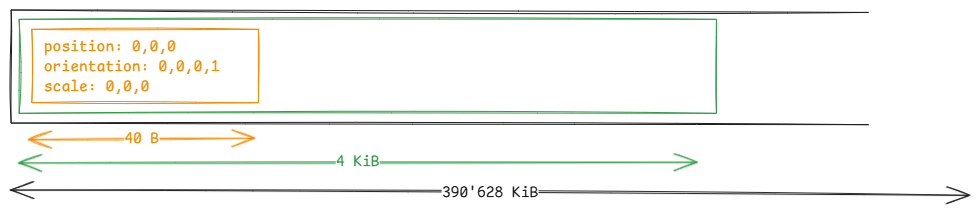
Around 382 MiB of address space is reserved, of which only 4 KiB is backed by physical RAM, of which only 40 bytes are used.

In this example, we will trigger an actual allocation of physical memory every 102 elements and the waste is limited to 4054 bytes. Note that we are not restricted to growing by one page at a time, we can grow by multiple pages if it makes more sense, but in that case we also increase the waste.

Computing the waste is straightforward:

MaxWaste = GrowFactor * PAGE_SIZE - sizeof(T)

---

All right, let's recap what we have so far:

• A virtual array with a fixed size that doesn't initially consume any physical memory.
• A way to grow the array by committing a new page worth of elements when the last committed page is full.
• A way to insert elements in place using a variadic template function.
• No pointer invalidation when adding elements to the array even if the array grows.

Even if virtual memory is relatively cheap, it's still not ideal to have an ever-growing array. Usually what's added needs to be removed at some point, so let's dive into the removal process.

Deletion

Removing elements is a bit trickier with our need to keep index stability and avoid pointer invalidation.

So, exit the swap-and-pop, and the shift strategies. We need a way to remove elements without touching anything else.

Using a freelist, we can avoid both of these issues.

A freelist is, as its name suggests, a data structure that keeps track of free elements in the array.

When we remove an element, we simply add its index to the freelist. When we add a new element, we check if the freelist is empty. If it is, we add the new element to the end of the array. If it's not, we take the first element from the freelist and use it as the new element.

This way, we can reuse the freed elements and avoid moving things around in the array.

Now the question is: how do we implement this?

The straightforward approach is to use a stack or queue of indices, but this involves more allocations which we want to avoid if possible.

If we take a look at a virtual array where we have removed a few elements, it would look something like this:

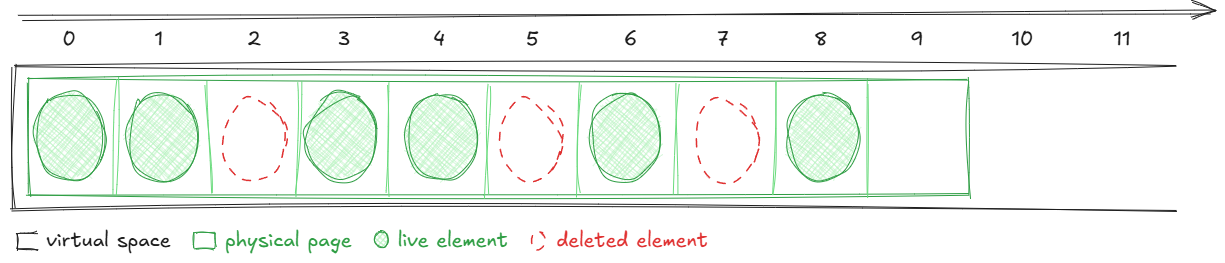
Notice that the freed elements leave holes in the array. Those holes are actually wasted committed memory. The freelist elements are simply the indices of those holes. So the idea is to use that memory to store those indices as an intrusive linked list.

We do that by simply adding a single size_t to our virtual_array class.

static constexpr auto FREELIST_EMPTY = size_t(-1);
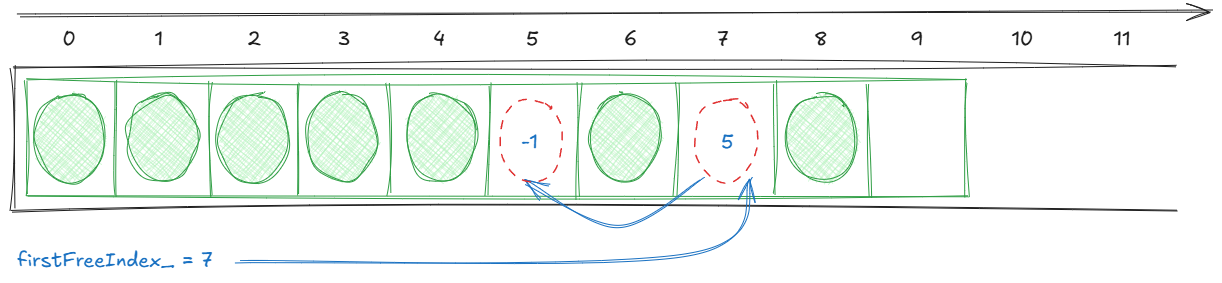
size_t firstFreeIndex_ = FREELIST_EMPTY;

Here's what a non empty freelist would look like:

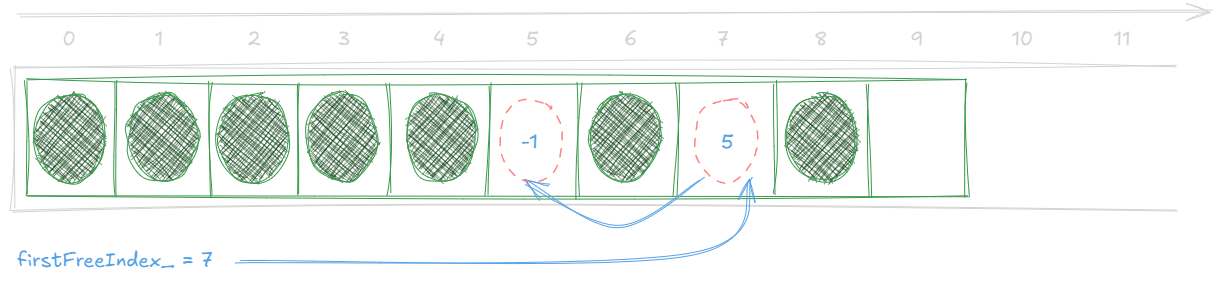
First of all, let's define a few helper functions to help us read and write the freelist indices:

size_t readFreeIndex(size_t freeIndex) {
    return *reinterpret_cast<size_t *>(pStart_ + freeIndex);
}

void writeFreeIndex(size_t freeIndex, size_t nextFreeIndex) {
    *reinterpret_cast<size_t *>(pStart_ + freeIndex) = nextFreeIndex;
}

pStart_ is of type T, we need to cast it to size_t * to be able to read and write the freelist indices. Using pointer arithmetic, given an index i, we can access the ith element of the array by simply doing pStart_ + i.

With this, pushing a new index to the freelist is as simple as:

void pushFreeList(size_t i)
{
    writeFreeIndex(i, firstFreeIndex_);
    firstFreeIndex_ = i;
}

We write the current first free index firstFreeIndex_ to the index we are freeing i, and then i becomes the new first free index.

Take the previous example, if we remove the element at index 2, we would end up with:

---

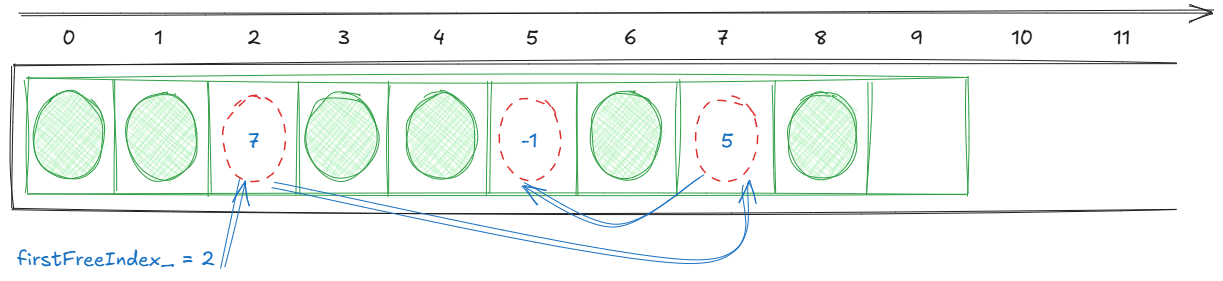
With this we have all we need to implement the remove function:

void remove(size_t i) {
    if constexpr (!std::is_trivially_destructible_v<T>()) {
        pStart_[i].~T();
    }

    pushFreeList(i);
}

Note that we only call the destructor if the type is not trivially destructible.

Now we are building the freelist but we're not using it yet.

Let's fix that.

Let's start by adding a function to pop the first element from the freelist if it's not empty:

size_t tryPopFreeList() {
    auto freeIndex = firstFreeIndex_;
    if (freeIndex != FREELIST_EMPTY){
        firstFreeIndex_ = readFreeIndex(freeIndex);
    }
    return freeIndex;
}

If the first free index is valid, we get its value, and replace it with the next free index by reading the element it's pointing to.

We just created an intrusive singly-linked list and used it as a stack (Last In First Out).

Now when we add a new element, we just try to pop the freelist. If the freelist had a valid index, we just return it and we're done. Otherwise we do as before.

size_t grabNextFreeIndex() {
    auto freeIndex = tryPopFreeList();
    if (freeIndex != FREELIST_EMPTY) {
        return freeIndex;
    }

    if (pCurrent_ == pLast_) {
        grow();
    }

    ++pCurrent_;
    return std::distance(pStart_, pCurrent_) - 1;
}

Finally, we need to update the emplace function to use the freelist:

template<typename... _Args>
T *emplace(_Args &&...args) {
    size_t freeIndex = grabNextFreeIndex();
    auto pNew = pStart_ + freeIndex;

    new (pNew) T(std::forward<_Args>(args)...);
    return pNew;
}

Et voilà!

We now have a virtual array that can grow automatically, doesn't invalidate pointers when we add elements to it, and is able to remove elements without moving things around.

But...

We created a new problem... The astute reader might have noticed that the destructor of the virtual_array class itself iterates over every element in the array and calls the element's destructor.

This worked because elements couldn't be removed otherwise. By introducing the removal we broke that assumption, some elements might already have been removed and their destructor already called.

We need a way to keep track of which elements are actually valid in the [pStart_, pCurrent_] range.

There's a few ways to do this, like adding a small header to each element, but that could be wasteful as all we really need is only a single bit of information. A more efficient approach is to use a bitset.

Validation

For a quick implementation we could use std::vector<bool> which is optimized for this usage, but it lacks some important guarantees like thread safety.

What we chose instead is to go with a simple array of uint64_ts, each uint64_t can hold the validity state of 64 elements. This array can be implemented using std::vector without too much trouble, as we don't need to worry about the pointer invalidation issue in this case.

std::vector<uint64_t> validityBits_;

If we take the Transform component as an example. Its size is 40 bytes, so we can fit 102 elements in a single page. So we need ceil(102 / 64) = 2 uint64_ts to hold the validity state of the elements in a single page. Say we reserve 10 million elements, we will need ceil(10'000'000 / 102) = 98'039 pages to hold the elements which translates to 98'039 * 2 = 196'078 uint64_ts to hold the validity state of the elements or roughly 1.5 MB.

This means that each time we grow the virtual array, we need to grow the validity state array by 2 uint64_ts.

Let's check the implementation, we start by modifying the grow() function to also grow the validity bits vector:

static constexpr size_t VALIDITY_REGISTERS_PER_PAGE =
        ELEMENTS_PER_PAGE / sizeof(uint64_t)
    +   ((ELEMENTS_PER_PAGE % sizeof(uint64_t)) == 0 ? 0 : 1);

void grow() {
    VirtualAlloc(pLast_, PAGE_SIZE, MEM_COMMIT, PAGE_READWRITE);
    pLast_ += ELEMENTS_PER_PAGE;

    validityBits_.resize(
        validityBits_.size() + VALIDITY_REGISTERS_PER_PAGE, 0ull
    );
}

Next up, we need to add a way to mark an index as used or unused:

void markIndexAsUsed(size_t i) {
    validityBits_[i / 64] |= (1ull << (i % 64));
}

void markIndexAsUnused(size_t i) {
    validityBits_[i / 64] &= ~(1ull << (i % 64));
}

This is basic bit manipulation, we compute the index of the validity register that holds the validity state of the element at index i by dividing i by 64 and we set (|=) or clear (&=) the i % 64th bit.

Now add a way to check the validity of an index:

bool isIndexValid(size_t i) const {
    return (validityBits_[i / 64] & (1ull << (i % 64))) != 0;
}

That's pretty much it. Now we need to update the emplace and remove functions to use the validity state array.

template<typename... _Args>
T *emplace(_Args &&...args) {
    size_t freeIndex = grabNextFreeIndex();
    auto pNew = pStart_ + freeIndex;

    new (pNew) T(std::forward<_Args>(args)...);
    markIndexAsUsed(freeIndex);

    return pNew;
}

void remove(size_t i) {
    markIndexAsUnused(i);

    if constexpr (!std::is_trivially_destructible_v<T>()) {
        pStart_[i].~T();
    }

    pushFreeList(i);
}

We can finally update the destructor to only destruct valid elements:

~virtual_array() {
    if constexpr (!std::is_trivially_destructible_v<T>()) {
        size_t i = 0;
        while (pCurrent_ != pStart_) {
            if (isIndexValid(i++)) {
                (*pCurrent_).~T();
            }
            --pCurrent_;
        }
    }
    VirtualFree(pStart_, 0, MEM_RELEASE);
    pStart_ = nullptr;
}

And we're finally done!

---

Performance Benchmarks

Let's take a look at how our virtual array performs compared to std::vector.

The benchmark is pretty simple, we create a virtual_array and a std::vector of Transform components and we measure the time it takes to insert 10 million elements in both of them. No preallocation is done for neither of them.

As a reminder, the Transform component is a POD struct with a size of 40 bytes, so 10 million elements will take up 400 MB of memory. Note that memory will be denoted in MB (1 MB = 1000 KiB) and not MiB (1 MiB = 1024 KiB).

These are of course synthetic tests that don't necessarily reflect real world usage, but they give a good idea of the different performance characteristics of the two approaches.

Here are the results:

Insertion

Insertion of 10M elements	Average	Min	Max	Gain	Memory Used	Memory Waste
std::vector<Transform>	250 ms	242 ms	268 ms	-	478.35 MB	+ 78.35 MB
virtual_array<Transform>	127 ms	113 ms	136 ms	x2	400 MB	+ 3.07 KB

std::vector pays the cost of dynamic reallocation: each growth step may involve allocating a larger buffer and copying existing data. On the other hand, virtual_array grows predictably and linearly, committing one page every 102 elements, and doesn't need to move anything around. That's a 2x speedup, with substantially less memory waste.

Removal

For deletion we fill both arrays with 10 million elements, then generate a randomized sequence of 10 million indices and we measure the time it takes to remove them one by one.

This is mostly a benchmark of removal strategies comparing the swap-and-pop versus freelist.

Removal of 10M elements	Average	Min	Max	Gain
swap-and-pop	150 ms	148 ms	160 ms	-
freelist	72 ms	70 ms	80 ms	x2

The freelist approach avoids the memory movement overhead of swap-and-pop. Every removal is just an 8 bytes write to the memory and a few bit manipulations. Again we see a 2x speedup.

Takeaways

• virtual_array gives us the speed of fixed-size arrays without locking us into a static size.
• Thanks to virtual memory, we can reserve a huge block of space upfront and only use real RAM when we actually need it.
• Deleting elements is fast and safe thanks to the freelist — no shifting, no pointer invalidation.
• The bitset makes sure we only run destructors on live elements, so cleanup stays safe and efficient.

All in all, it's faster, leaner, and more predictable than a std::vector, especially when you're working with millions of items.

But we've only scratched the surface, this is still just one thread doing all the work. Next up, we'll take virtual_array into multi-threaded territory and see how it holds up under real pressure.